物体的受力平衡

1.共线力系的平衡

若一个力系作用于物体时不发生任何外效应，则受此力系作用的物体处于平衡状态。物体要处于平衡状态,除了不能有任何方向的移动外,还必须是绕任意一点都不能转动。所以，物体受力平衡时必须满足:①力系中各力沿任一方向的分力的代数和应等于零;②力系中各力对于任意一点(或轴)的力矩的代数和应等于零。

最简单的平衡状态是物体在两个力作用下的平衡。根据二力平衡定律,若两个力使物体平衡，则此二力必须大小相等、方向相反,且作用在同一直线上,如图1所示。其平衡方程式为

∑F=0

并且各力对力的作用线以外任意-点A的力矩的代数和等于零,即

∑M_A(F)=0

满足以上两个平衡方程式之中的任何一个,都能保证力系的平衡。显然,此平衡条件可推广应用于共线力系中任意力作用下物体的平衡,故共线力系的平衡只有一一个独立平衡方程式。

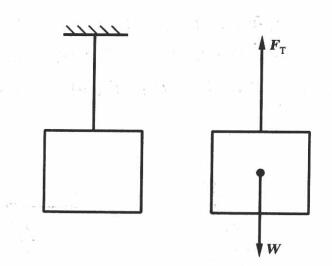
图1二力作用下物体的平衡

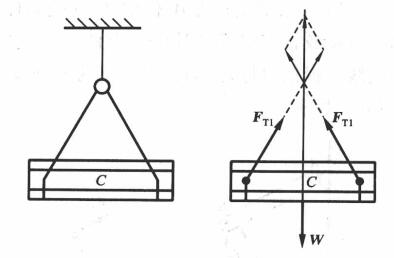
图2平面内三 力作用下物体的平衡

2平面力系的平衡

对于平面力系，假如在一个平面中某- -物体受到不共线的三个力的作用,如图2所示，要使得物体平衡,其中两个力的合力必须与第三个力的大小相等、方向相反，也就是三个力的合力为零。由此可知,在平面力系中,不论有多少个力作用于物体上,使物体平衡的必要条件都是各力的矢量和为零,即

∑F=0

也就是各力在平面坐标系x、y两轴上投影的代数和均等于零，即

∑F_x=0，∑F_y=0

但力系仅满足合力等于零的条件,还不一-定能使物体平衡。假如当三个力作用于物体上时,两个力的合力与第三个力大小相等、方向相反,但不共线,会形成一个力偶。即力系对力的作用线以外任一点(或轴)的力矩和不等于零,亦即存在一个力偶矩,这时物体可产生转动效应而不能平衡。故平面力系除了必须满足在平面坐标系x、y两轴上投影的代数和均等于零外，还应具备另一条件,即各力对平面内任意一点O的力矩和也等于零,即

∑Mo(F)=0

故平面力系平衡的代数条件为

∑F_x=0，∑F_y=0，∑M_o(F)=0

3空间力系的平衡

对于空间力系而言，由于各力的作用线并不在同一个平面内,如仅满足上述平面力系中的三个平衡方程式,并不能保证物体平衡。如图1-19所示,在空间力系作用下的物体仍然可以沿着z轴移动和转动。由此可知,要使在空间力系作用下的物体平衡,必须使物体在沿三条相互垂直的轴线方向上都没有移动，同时还必须使物体没有绕Ox,Oy,Oz三根轴的转动。为此,必须相应地具有六个平衡条件，即各力在x,y,z三轴方向投影的代数和等于零,绕Ox,Oy,Oz三轴的力矩和等于零,由此得出空间力系的代数条件为

∑F_x=0，∑F_y=0，∑F_z=0

∑M_z(F)=0，∑M_y(F)=0，∑M_z(F)=0

而对于空间上的共点力系,只要各力在相互垂直的三轴上投影的代数和均为零，则各力必平衡,即空间共点力系的三个平衡方程式为

∑F_x=0，∑F_y=0，∑F_z=0

而对于空间上的平行力系,只要各力沿与其平行的轴线方向(如z轴方向)的代数和等于零,且各力对于与其不平行的两轴的力矩和均为零,则此力系必平衡，即此空间平行力系的三个平衡方程为

∑M_z(F)=0，∑M_y(F)=0，∑M_z(F)=0

对于平面力系和空间力系,在建立平衡方程时,若能适当选择分力的方向与力矩中心(或轴)的位置,使所得到的每个平衡方程式都只含有一个未知量,则无需联立求解,计算工作量可以大为简化。平面一般力系的静力方程式中具有三个未知量。若能选择两个未知力的交点作为矩心,则写出的一个力矩方程式中就仅包含一个未知力,无需联立即可得出次未知力与已知力的关系。