点在两投影面体系中的投影

如图1所示为空间两个互相垂直的投影面,处于正面直立的投影面称为正投影面，用V来表示，简称V面;处于水平位置的投影面称为水平投影面,用H来表示,简称H面;由V面和H面所组成的体系称为两投影面体系。V面和H面的交线称为X投影轴,简称X轴。

H、V两投影面将空间划分为四个部分,每一个部分称为一个分角。H的上半部分,V的前半部分称为第一分角;H 的上半部分,V的后半部分称为第二分角;H的下半部分,V的后半部分称为第三分角;H的下半部分,V的前半部分称为第四分角;它们依次用I、II、I、IV表示。

1.点的两面投影图

首先来研究点在第一分角内的投影。

如图2(a)所示,过空间一点A向H面作垂线,其垂足a就是点A在面H上的投影,称为点A的水平投影,以a表示。再由点A向V面作垂线,其垂足a'就是点A在面V上的投影，称为点A的正面投影,以a'表示。
为了统一,规定空间点用A,B,C,…大写字母表示;水平投影用相应的小写字母a, b,c,..表示;正面投影用相应的小写字母在右上角加一撇a',b',c',..表示;侧面投影用相应的小写字母在右_上角加两撇a",b" ,c" ,表示。

图1两投影 面体系

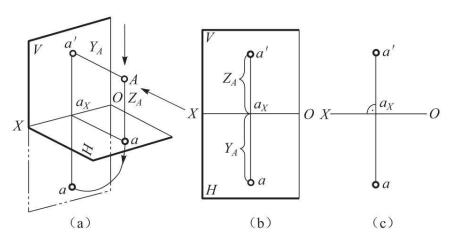
图2点在第一分角中的投影

为了便于作图,需要把位于两个互相垂直的投影面内的投影展开到一个平面内。规定V面保持不动,将H面绕X轴向下旋转90°与V面重合,即处于同一平面上，得到的两面投影图如图2(b)所示。因为投影面可根据需要来扩大,故此通常不必画出投影面的边界，图2(c)为去掉边框后点A的投影图。

反之,如果有了点的正面投影和水平投影,就可以确定该点的空间位置。

2.两面投影图中点的投影规律

在图2(a)中,Aaaxa'是个矩形,a'a_x⊥X轴,aa_x⊥X轴,H面绕X轴向下经旋转90°后，a,a'的连线aa'一定垂直于X轴,由此可得出点的投影规律:

(1)点的水平投影和正面投影的连线垂直于X轴,即aa'⊥X轴。

(2)点的水平投影到X轴的距离等于空间点到V面的距离,即aa_x =Aa'。

(3)点的正面投影到X轴的距离等于空间点到H面的距离,即a'a_x=Aa。

3.其他分角中点的投影

应当指出，上述点的投影规律对于其他分角的点的投影也是适用的。如图3(a) 所示,空间点B,C,D分别处于II、I、IV分角中,各点分别向相应的投影面作投影线，就可以得到各点的正面投影和水平投影。当前半部分的H面向下旋转90°(亦即后半部分的H1面向上旋转90°)与V面(V1面)重合后得到各点投影图(图3(b))。显然,这些点的投影也必定符合上述投影规律,但各点的投影在图上的位置有如下的特点:

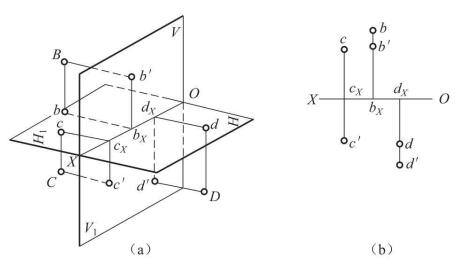
图3 其他分角中点的投影

第I分角中的点B,正面投影b'和水平投影b同在X轴的上方。

第II分角中的点C,正面投影c'在X轴的下方,水平投影c在X轴的上方。

第IV分角中的点D,正面投影d'和水平投影d同在X轴的下方。

注意，上述各点在各分角中的投影位置，在前半部分的H面向下旋转90°和后半部分的H面向上旋转90%后,分别与V1面和V面重合后标出的。理解点B,C,D的投影位置时,务必注意此点。

4.投影面和投影轴上点的投影

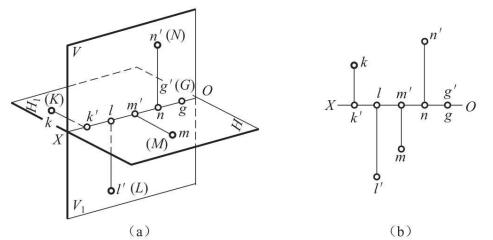
图4 投影面和投影轴上的点的投影

在特殊情况下,点也可以处于投影面上和投影轴上，如图4(a)所示。点在哪个投影面上,它距这个投影面的距离即为零，并且与该投影面上的投影重合,而另--投影在投影轴上,如图4(b)所示。如点M在面H上,则m与M重合，m'在X轴上,同理点K也如此。点N在面V上,则n'与N重合，同理点L也如此。
当点在投影轴.上时,它的两个投影均与空间点重合在投影轴上。如点G在X轴上，则g,g'与G均重合在X轴上。