点在三投影面体系中的投影

1.点的三面投影图

如图1(a)所示,在两投影面体系的基础上再加上-个与H,V均垂直的投影面,使它处于侧立位置,称为侧立投影面,以W表示,简称W面,这样3个互相垂直的H,V, W面就组成了一个三投影面体系。H, W面的交线称为Y投影轴,简称Y轴;V, wW面的交线称为Z投影轴,简称Z轴,3个投影轴的交点0称为原点。

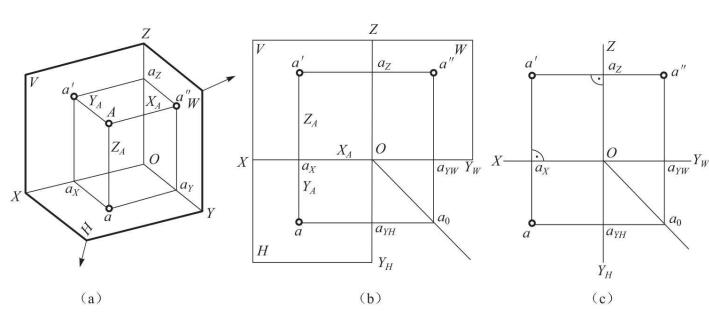
图1点在三投影面体系中的投影

将空间一点A分别向H,V, W面进行投影得a, a' ,a"，则a"称为点A的侧面投影。分别将H,W面按图示箭头方向旋转，使H,W面与V面处于同一个平面,即得点的三面投影图,如图1(b)所示。其中Y轴随H面旋转时,以YH表示;随W面旋转时,以Yw表示。一般在投影图上只画出其投影轴,不画出投影面的边界。

2.点的直角坐标与三面投影的关系

如果把三投影面体系看做空间直角坐标系,则H,V,W面即为坐标面,X,Y,Z轴即为坐标轴,点0即为坐标原点。由图1可知,点A的三个直角坐标X_A,Y_A,Z_A即为A点到3个坐标.面的距离,它们与A点的投影a,a' ,a"的关系如下:

Aa" =aa_Y =a'a_z=Oa_x=X_A

Aa' =aa_x=a"a_z=Oa_y=Y_A

Aa=a'a_x=a"a_y=Oa_z=Z_A

由此可见:点A的水平投影a由Oa_x和Oay,即点A的X_A,Y_A两坐标确定;正面投影a'由Oa_x和0az,即点A的X_A,Z_A两坐标确定;侧面投影a”由Oa_y和Oa_z,即点A的Y_A,Z_A两坐标确定。

结论:空间点A(X_A,Y_A,Z_A)在三投影面体系中有唯一的一组投影(a, a' ,a"),反之，如已知点A的一组投影(a, a',a") ,即可确定该点在空间的坐标值。

3.点在三投影面体系中的投影规律

通过上面的分析及两投影面体系中点的投影规律,可以得出三投影面体系中点的投影规律:

(1)点的正面投影和水平投影的连线垂直于X轴。这两个投影都反映空间点的X坐标，即aa'⊥X轴,a'a_z =aa_yh=X_A(点到面W的距离)。

(2)点的正面投影和侧面投影的连线垂直于Z轴。这两个投影都反映空间点的Z坐标，即a'a"⊥Z轴,a'a_x =a"a_yw=Z_A(点到面H的距离)。

(3)点的水平投影到X轴的距离等于侧面投影到Z轴的距离。这两个投影都反映空间点的Y坐标，即aa_X=a"a_z=Y_A(点到面V的距离)。

如图1(c)所示,由于Oa_YH =Oa_YW ,作图时可过点O作直角∠Y_HOY_w的角平分线,它与Y_H或Yw成45°,从a引X轴的平行线与角平分线相交于a₀,再从a₀引Yw的垂线与从a'引Z轴的垂线相交,其交点为a"。

根据点的投影规律,可由点的3个坐标值画出其三面投影图,也可以根据点的两个投影作出点的第三投影。