(1)切平面。曲面E上过M点的各曲线的切线皆位于同一平面上,称为M点的切平面,记为π (图1)。
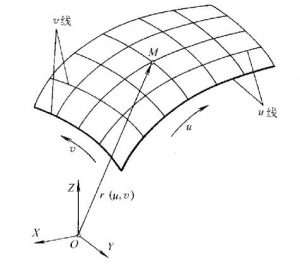
图1切平面
(2)法线。在曲面的M点处,过M点对该点的切平面作垂线,称为M点的法线。记为n (图2)。
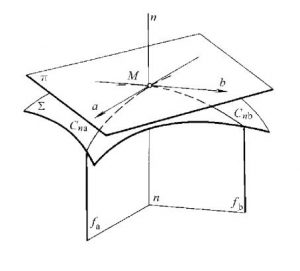
图2M点的法线
(3)法截面、法截线。过法线所作曲面的截平面,称为法截面,如图5中的J、f面。法截面与曲面的截交线称为法截线。如图中的Cna、 Cnb。
(4)法曲率。法截线在M点处的曲率,称为法曲率。如图2中法截线C.. C的法曲率为k. k。它们分别对应的切线方向称为该法曲率的方向,如图中的a、b.
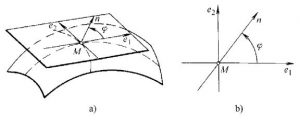
图3法曲率
(5)主方向。过M点的各切线方向中,对应法自本具有极大值或极小值的方向,称为主方向。一般有两个主方向,分别记为e1、e2,并且e1⊥e2 (图3a)。
(6)主曲率。对应于主方向的法曲率值,称为主曲率。分别记为k1、k2。
(7)总曲率(高斯曲率)。在曲面上的点M处,它的两个主曲率的乘积,称为M点的总曲率,记为K,K=k1k2。K值可用于擂述曲面在点M处的弯曲性质。
(8)欧拉公式。曲面上M点处任:方向的法曲率和两个主曲率的关系,可用欧拉公式表示:
kn= k1cos2φ+ k2sin2φ
其中,kn为对应n方向的法曲率,4为n方向与主方间e1的夹角(图3b)。



