1已知长、短轴,作椭圆
例1: 己知椭圆的长轴AB、短轴CD,作椭圆(图1)。

图1已知椭圆长、短轴AB及CD找出椭圆的焦点F1、F2后,再作椭圆
作图步骤:
(1)以长、短轴为直径作两个同心的辅助圆;
(2)在两辅助圆上作出对应的等分点,如1、2、3、...及1'、2'、3'、..... (等分数量随精确度要求而定);
(3)依次自等分点1'、2'、...作铅垂线,同时自对应的等分点1、2、...作水平线;
(4)各铅垂线与其对应的水平线的交点P1、P2、P3、......椭圆曲线上的点,从而可以作出椭圆。
例2:已知椭圆长、短轴AB及CD,找出椭圆的焦点F1、F2后,再作椭圆(图 2)。

图 2已知椭圆长、短轴AB及CD找出椭圆的焦点F1、F2后,再作椭圆
作图步骤:
(1)以短轴端点D为圆心,R=1/2AB为半径作辅助圆与AB交于F、F。(即焦点);
(2)将OF1、OF2分为相应的若干分段,如F11、12、23、...及F21'、1'2'、2'3'、 .... (靠近F1、F2处分段宜较密);
(3)以F1为圆心,依次以A1、A2.....为半径作弧;以F2为圆心,依次以B1、B2、....为半径作弧;
(4)两对应弧的交点P1、P2、P3、...即为椭圆曲线上的点,从而可以作出椭圆。
例3:己知椭圆的长、短轴AB、CD,用四心扁圆的方法作椭圆(近似作图)(图3)。

图3己知椭圆的长、短轴AB、CD,用四心扁圆的方法作椭圆近似作图
作图步骤:
(1)在短轴CD线上取0K=0A,得点K;
(2)连接A、C,在AC线上取CK'=CK,得点K';
(3)作AK'的中乘线,交OA于0),交O)D于02;
(4)作O3、0。,分别与0,、0):对称于长、短轴线;
(5)以0,02、03、0,为圆心,分别以O、A、02C、O。B、0,D为半径作四段圆弧,即为近似椭圆一扁圆
2已知共轭轴,作椭圆

图4已知共轭轴,作椭圆
方法1 (图4a)
作图步骤:
(1)以共轭轴MM为直径作辅助圆;
(2)过MM1上的各点1、2、....作MM的垂线与辅助圆相交于点1'、2'、 3....
(3)连接过圆心0所作垂线的交点5'与另共轭轴NN;的端点N;
(4)过点1'、2'、3'、....作5'N的平行线,再过点1、2、3、...作NN;的平行线,相应两平行线的交点P、P:、P。、.....为椭圆曲线上的点。
方法2 (图4b)
作图步骤:
(1)过共轭轴的各端点N、N、M、M作平行四边形EFGH (其对边分别平行于MM1及NN1);
(2)在OM、OM及其相邻边HM、GM上作同数口的等分点1、2、3、....及.. 1'、2'、3'、.... ;
(3)从NN1的一个端点N1出发,过MM1上的等分点1、2、3、4、5、6作射线;再从另端点N出发向HM,GM1各等分点1'、2'、3'、4'、5'、6'作射线。两组射线中两相应射线的交点P、P2、....即椭圆曲线上的点。
3 确定椭圆长、短轴的方向和大小
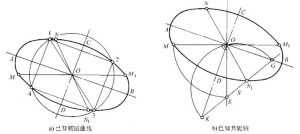
图6确定椭圆长、短轴的方向和大小
图6a为已知椭圆曲线的作图步骤:
(1)以点O为圆心,任作一圆与椭圆相交于点1、2、3、4;
(2)矩形1234的对称中心线即为椭圆的长、短轴的方向,与椭圆曲线交点的连线AB、CD即为椭圆的长、短轴。
图6b为己知共轭轴MM1,NN1的作图步骤:
(1)作OE⊥MM,并使OE=OM;
(2)连接E及N1,以EN1的中点S为圆心,OS为半径作弧,与EN1的延长线相交于G、K两点;
(3) OG为椭圆的长轴方向,长轴的长度为2EG; OK为短轴方向,其长度为2KE。
4 作椭圆曲线上的切线及法线.
例1:己知椭圆曲线及线上:点T,作椭圆的法线和切线(图7)。
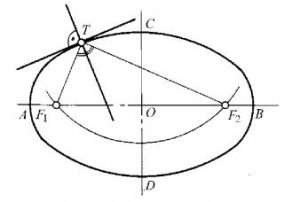
图7作椭圆曲线上的切线及法线
作图步骤:
(1)以短轴端点C为圆心,长轴之半OA为半径作弧,交AB于F1、F2(即焦点);
(2)连接F1T和F2T;
(3)作∠F1TF2的角平分线,即椭圆上点T处的法线;
(4)过点T作法线的垂线,即其切线。
例2:过椭圆外一点s作椭圆的法线(图8)。
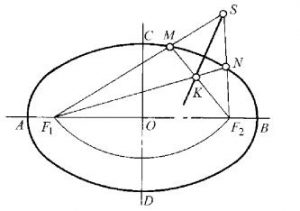
图8过椭圆外一点s作椭圆的法线
作图步骤:
(1)先求出椭圆的焦点F1、F2;
(2)作连线F1S及F2S.分别与椭圆交于M及N;
(3)两连线F1N及F2M相交于K,KS即为所求的法线。
例3:过椭圆外一点S作椭圆的切线(图9)。
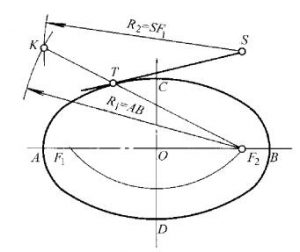
图9过椭圆外一点S作椭圆的切线
作图步骤:
(l)先求出椭圆焦点F1、F2;
(2)以F2为圆心,长轴AB为半径作弧;
(3)再以S为圆心,SF1为半径作弧,两弧相交于K;
(4)KF2与椭圆相交于T,直线ST即为所求的切线
5 作椭圆的展开长度(近似作图) (图10)
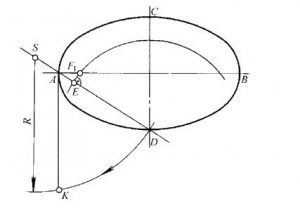
图10 作椭圆的展开长度近似作图
作图步骤:
(1)求出椭圆的一个焦点F1;
(2)连接椭圆长、短轴端点D、A;
(3)过F1作F1E⊥DA,在DA延长线上量取AS=1.5AE;
(4)以S为圆心、SD为半径作弧,与过A点所作铅垂线(切线)相交于K,AK即为AD曲线段的展开长度(近似)。



