投射线互相平行的投影法称为平行投影法。
投射线倾斜于投影面的投影方法,称为斜投影法。用这种方法所得的投影称为斜投影。
投射线垂直干投影面的投影方法称为正投影法。用这种方法所得的投影称为正投影,简称投影。
由于采用正投影法在投影图上容易表达空间物体的大小,度量性好,作图方便,生产中的机械图样大都是采用正投影法绘制的,因此,正投影法是机械制图的主要理论基础。
研究投影的基本性质目的在于研究空间几何要素与其投影之间的一一对应关系。其中主要研究哪些空间几何特征在投影图上保持不变,哪些空间几何特征产生了变化和如何变化,以作为画图和看图时的依据。下面简述平行投影的--些基本性质。
1.不变性
(1)一般情况下,直线的投影仍为直线,曲线的投影仍为曲线。如图1所示。
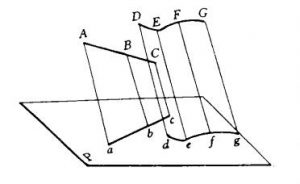
图1直线和曲线的投影
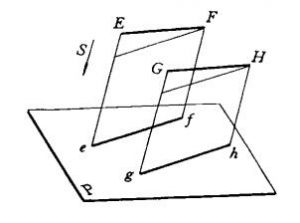
图2平行线段的投影
(2)两平行线段的投影仍互相平行。如图2所示,设EF//GH,由于Ee//Ff//Gg//Hh,故口EefF//DGghH ,所以ef//gh。
(3)平行于投影面的任何线段或平面图形。其投影反映线段实长或图形的实形。如图3所示,若MN//P,则mn=MN。因为MN//P,则MNnm为一平行四边形,所以mn=MN。又因△ABC//P,即△ABC的每边平行于P面,故△ABC在P画上的投影反映实形。
2.积聚性
当空间直线或平面所处位置与投射线平行时,则直线的投影积聚为一点,平面的投影积聚成一直线,这种性质称为积聚性。图3中平面曲线L和平面ABCD的投影在平面P上都积聚为一条直线,直线AB和CD都积聚为一点。
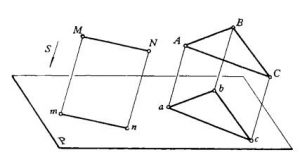
图3平行于投影面的直线和平面的投影
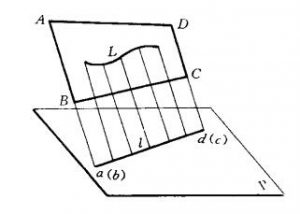
图4投影的积聚性
3.从属性
设点在直线上,则该点的投影必在直线的同面投影.上,如图1所示,点B在直线AC.上,其投影b点在ac上。
4.等比性
(1)直线上的一点将该直线分成两段,该两线段之比,等于其投影之比。如图2.5所示,由于Aa//Bb/Cc,故有AB:BC= ab:bc。
(2)空间两平行线段之比,等于其投影之比。如图2.6所示,分别过F和H作fe和hg的平行线,于是得到两个相互平行的相似三角形及矩形,根据相似三角形对应边成比例和矩形对边相等的关系可得到EF:GH=ef:gh.



