在一组尺寸链中,从形式上看各个环都一样,但其中有些环是代表着机器的装配要求,需要从机器的性能或者工作质量来确定其数值。例如图1-1所示的尺寸链中,装配后形成的轴向间隙,是影响机器运转平稳性的主要环节,它代表着这个箱体的装配要求。作为机器的通用技术要求,回转轴的轴向间隙约为0.1~0.3mm。除代表整个机器或构件装配要求的特定环外,其他环掷可看作是影响装配质量的因素,它们的制造误差累积起来将影响装配质量。
例如图1中,A1、A......各个尺寸误差将影响ΔN的大小,因 此是影响装配要求的组成部分。
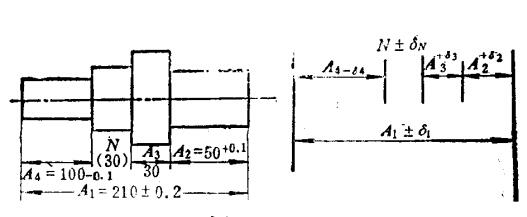
图1 尺寸链
从图1可以看到,在一个单独的零件上,各个尺寸之间也存在着误差的相互影响和积累,有些尺寸已经明确标注,可以在加工制造时直接控制尺寸误差,如图1中 A1、A2、A3和A4。但有些尺寸是间接封闭而形成的,如图1中的尺寸N。尺寸A1、A2、A3和A4的制造误差累积后将影响封闭尺寸N,产生误差δN。
以上这种组成尺寸之间的相互影响关系,也就是“组成环”和“封闭环”之间的影响关系,不管在任何情况下,组成环误差将累积在封闭环上,累积后形成封闭环的误差。
由于在组成环中有增环和诚环的区别,因此它们对封闭环的影响状况也就不一样,其区别为:增环对封闭环误差的积累关系为同向影响,增环误差增大(或减小)可使封闭环尺寸相应的一同增大(或减小)。而且使封闭环尺寸向偏大方向偏移。
减环对封闭环误差的积累关系为反向影响,减环误差增大(或减小)可使封闭环尺寸相应的反而减小(或增大)。而且使封闭环尺寸向偏小方向偏移。
但是增环尺寸增大使封闭环向偏大方向偏移,减环又使封闭环向偏小尺寸方向偏移,综合起来、结果使封闭环尺寸向两个方向扩大,最后使封闭环误差δN增大。因此由图2即可看出,组成环中、包括所有的增环和减环,都最终将影响封闭环误差增加。
根据前面所举的例子间以看出,不论尺寸链的组成环有多少,也不管它的形式和用途怎样,都是反映着封闭环和组成环之间的相互影响关系。而这种相互影响关系也正是尺寸链所代表的基本关系。
尺寸链所代表的基本关系是用来说明尺寸链的基本原理和本质问题的,在建立尺寸链的基本概念中具有十分重要的意义。为了说明内在因素的影响关系,还可用图2的一般尺寸链来进行说明。
图2说明了各组成环尺寸都有一定的误差土δi,所以封闭环受各组成环误差的影响,可能产生极大值Nmax;另一方面,在相反的极限情况下也可能产生极小值Nmin。
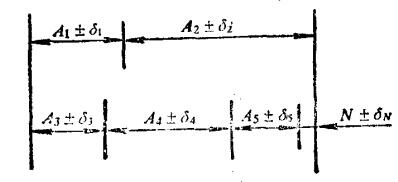
图2
封闭环产生最大极限尺寸的情况为:
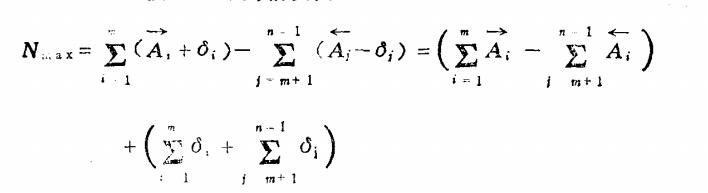
封闭环产生最小极限尺寸的情况为:
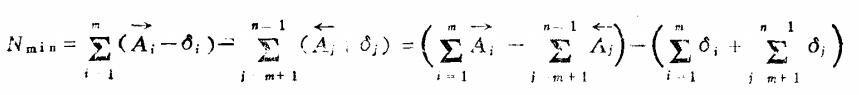
式中
![]() 组成环中的增环,
组成环中的增环,
![]() 组成环中的减环;
组成环中的减环;
δi和δj—组成环的公差;
n—尺寸链的总环数,( 包括封闭环);
m—尺寸链中的增环数;
(n-1)—尺寸链中组成环数;
Nmax—封闭环最大极限偏差;
Nmin—封闭环最小极限偏差。
由于(Nmax- Nmin)为封闭环的公差,因此把公式(1-1)和(1-2)相减则得:

在上式中,δi和δj都是尺寸链的组成环,如果用δi来代表所有各组成环的公差则得:

最后推导出的这个公式,说明了封闭环偏差为各组成环公差的代数和。这个式子所代表的关系就是尺寸链误差的综合关系式。这个误差关系式对任何的机器结构,对任何类型的尺寸链,以及任何生产过程中的应用都是适用的。它在尺寸链的分析计算中具有普遍的意义,因此把它叫做尺寸链的基本关系式。
对尺寸链单纯理解为封闭的尺寸组合是很不全面的,由尺寸链的基本关系式可揭示尺寸链的本质,是组成环误差的综合关系。
通过上面的分析,对尺寸链所代表的基本关系可以总结为以下三点:
1)尺寸 链中各环组成封闭的形式。这一点由图1-4的组合关系可以看出,各个增环和各个减环形成封闭的框图。各环之间具有封闭性。
2)在尺寸链中, 增环尺寸的总和等于减环尺寸和封闭环尺寸之和。即:
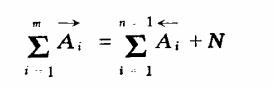
3)在尺寸链中,封闭环的偏差等于各组成环公差之和。
以上三点中最主要的是误差综合关系,这-关系一方面说明当各组成环公差已经确定时,组成环公差之和即形成了封闭环的偏差;另一方面,当封闭环偏差根据机器的精度标准已经明确确定时,组成环公差的允许值也就有了--定的限制。各组成环的公差是互相影响,相互补偿,而又相互制约的。某些环允许的公差有所增大,同时也就意味着另--些组成环允许公差的相应减小。这种封闭环偏差和组成环公差之间的相互影响,同时又相互制约的特点,也正是尺寸链所表示的本质性问题。
尺寸链的基本原理,主要是反映误差的综合和累积的,以后各种计算公式都是依此基本关系推演转化而建立的。因此应当由此建立尺寸链的基本概念,然后再熟悉各种计算公式的应用,这一点对于掌握尺寸链的分析问题方法是十分重要的。



